The Forces of Nature by Kelland Terry, Ph.D.
As explained in the previous blog, it requires more energy than expected to accelerate an electron in a particle accelerator. This is particularly true the closer the particle comes to the speed of light. How does VES ether theory solve this puzzle?
First, only those gravitons traveling along the surface of Earth will have an appreciable affect on the particle in the accelerator because those emanating from the ground beneath the accelerator will strike the particle’s waves at 90 degrees to its line of flight or at some other sharp angle. Earth’s gravitons will have far less impact on electron velocity compared to those traveling parallel to the surface of Earth and in line with the accelerator. For this reason, we can assume that an equal number of graviton waves are traveling with and against the subatomic particle being accelerated.
I invite you to go to my blog of 2/2/12 if you choose to review what to expect when balls or waves with perfect elasticity strike each other.
Graviton waves traveling against the flight path of the particle act as negative forces because they impede string retraction and they impede the flight of the electron. At the same time, those waves going in the same direction as the electron in flight act as positive forces. They are the strings responsible for pushing the electron through space, and they tend to increase the rate of string cycles.
The dynamics between these two opposing forces are responsible for normal velocity of electrons in orbit, which is 2 x 10^6 meters per second. However, the dynamics between the forces change dramatically as the electron is forced to travel at the speed of light. I will continue with this discussion in my next blog. Till then be safe and in good health. Kelland—www.vestheory.com
Monday, February 20, 2012
Thursday, February 16, 2012
Electrons in particle accelerators
The Forces of Nature by Kelland Terry, Ph.D.
The velocity of an electron in orbit is 2 x 10^6 meters per second, and somewhat less in the solar wind. To increase the velocity of these particles beyond this point requires a source of energy. This has been examined in particle accelerators.
It has been proven that the acceleration of the electron requires more energy than expected. It is as if the mass of the particle increases as it approaches the speed of light; however, the mass remains the same.
Relative momentum = (gamma) x mass x velocity
Gamma is the reciprocal of the Lorentz factor as previously discussed, and it is always greater than one, which means “relative” momentum is always greater than mass x velocity.

Gamma reflects the additional energy required to raise the electron to a specified velocity. It is a measure of the resistance met by the electron as it is accelerated. In this equation, v is the velocity of the electron in the accelerator and c is the velocity of light. Gamma increases dramatically as the speed of light is approached. This is shown in the next illustration.
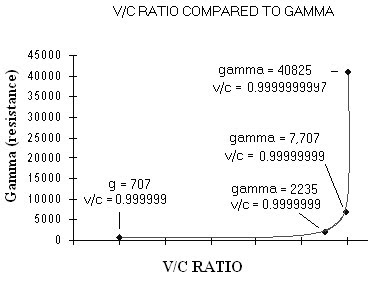
In this illustration, V/C is the ratio of the observed velocity V divided by the velocity of light, C.
As gamma increases from 707 to 40,825 (57.7 fold increase), the velocity of the electron only increases 1.000000999701 fold. Obviously, if the velocity of the electron had increased according to the energy applied, its velocity would have been 57.7 fold greater. This didn’t happen because increasing the velocity of the electron meets with great resistance.
If we live in a three-dimensional world, the question becomes: What is the source of resistance that must be overcome to increase the velocity of the electron? This question can be answered using elastic string theory. Till then be safe and in good health. Kelland—www.vestheory.com
The velocity of an electron in orbit is 2 x 10^6 meters per second, and somewhat less in the solar wind. To increase the velocity of these particles beyond this point requires a source of energy. This has been examined in particle accelerators.
It has been proven that the acceleration of the electron requires more energy than expected. It is as if the mass of the particle increases as it approaches the speed of light; however, the mass remains the same.
Relative momentum = (gamma) x mass x velocity
Gamma is the reciprocal of the Lorentz factor as previously discussed, and it is always greater than one, which means “relative” momentum is always greater than mass x velocity.

Gamma reflects the additional energy required to raise the electron to a specified velocity. It is a measure of the resistance met by the electron as it is accelerated. In this equation, v is the velocity of the electron in the accelerator and c is the velocity of light. Gamma increases dramatically as the speed of light is approached. This is shown in the next illustration.

In this illustration, V/C is the ratio of the observed velocity V divided by the velocity of light, C.
As gamma increases from 707 to 40,825 (57.7 fold increase), the velocity of the electron only increases 1.000000999701 fold. Obviously, if the velocity of the electron had increased according to the energy applied, its velocity would have been 57.7 fold greater. This didn’t happen because increasing the velocity of the electron meets with great resistance.
If we live in a three-dimensional world, the question becomes: What is the source of resistance that must be overcome to increase the velocity of the electron? This question can be answered using elastic string theory. Till then be safe and in good health. Kelland—www.vestheory.com
Wednesday, February 15, 2012
Basic equations used by the special theory of relativity
The Forces of Nature by Kelland Terry, Ph.D.
The special theory of relativity states that time slows down for an object in motion. This means that a clock in motion will actually tick fewer times per second compared to a stationary reference clock because length between ticks is greater. This is spoken of as time dilation. Einstein used the Lorenz equation to define this belief in the following way:
Time dilation
Relativistic time = normal time x gamma.
Where gamma is the inverse of the Lorentz contraction:

Because gamma is always greater than one, relativistic time is always greater than normal time. I will return to this equation when I discuss objects in motion in another section.
Relativistic momentum
The energy required to increase the velocity of an electron to the speed of light is much greater than expected. At one time it was thought that the mass of the particle increased, but this is no longer thought to be the case. The resistance to any increase in the speed of the particle follows gamma.
The special theory of relativity views this as an increase in momentum, which is calculated as follows:
Relativistic momentum = gamma x velocity x mass
This equation actually tells us that it requires more energy than expected to increase the velocity of the electon in a particle accelerator, not that the mass changes. I will return to this equation when I discuss particle accelerators.
Einstein reasoned that these equations can only apply if we live in a four dimensional world rather than the normal three: length, depth, and height. The forth dimension is time, which explains time dilation and the effect of motion on time and particles in motion.
According to relativity theory, the original concept of the Lorentz contraction still applies, although they prefer to state that space shrinks:

This theory does lead to the curious assertion that a large particle accelerator in use shrinks to a few meters.
Is there another way of explaining the odd behavior of particles in motion without invoking a four dimensional world? I believe so. I will begin to tackle this subject in my next blog. Till then be safe and in good health. Kelland—www.vestheory.com
The special theory of relativity states that time slows down for an object in motion. This means that a clock in motion will actually tick fewer times per second compared to a stationary reference clock because length between ticks is greater. This is spoken of as time dilation. Einstein used the Lorenz equation to define this belief in the following way:
Time dilation
Relativistic time = normal time x gamma.
Where gamma is the inverse of the Lorentz contraction:

Because gamma is always greater than one, relativistic time is always greater than normal time. I will return to this equation when I discuss objects in motion in another section.
Relativistic momentum
The energy required to increase the velocity of an electron to the speed of light is much greater than expected. At one time it was thought that the mass of the particle increased, but this is no longer thought to be the case. The resistance to any increase in the speed of the particle follows gamma.
The special theory of relativity views this as an increase in momentum, which is calculated as follows:
Relativistic momentum = gamma x velocity x mass
This equation actually tells us that it requires more energy than expected to increase the velocity of the electon in a particle accelerator, not that the mass changes. I will return to this equation when I discuss particle accelerators.
Einstein reasoned that these equations can only apply if we live in a four dimensional world rather than the normal three: length, depth, and height. The forth dimension is time, which explains time dilation and the effect of motion on time and particles in motion.
According to relativity theory, the original concept of the Lorentz contraction still applies, although they prefer to state that space shrinks:

This theory does lead to the curious assertion that a large particle accelerator in use shrinks to a few meters.
Is there another way of explaining the odd behavior of particles in motion without invoking a four dimensional world? I believe so. I will begin to tackle this subject in my next blog. Till then be safe and in good health. Kelland—www.vestheory.com
Tuesday, February 14, 2012
The Michelson-Morley Experiment
The Forces of Nature by Kelland Terry, Ph.D.
Albert Einstein published his special theory of relativity in 1905. This theory has been used to explain the odd behavior of electrons and radioactive particles in particle accelerators, the strange behavior of atomic clocks and radioactive particles in motion, and other curious phenomenon involving photons. I will come back to these observations after I discuss the origin of the equation that forms the backbone of special relativity.
The theory of relativity has its roots in an experiment carried out by A. Michelson and E. W. Morley in 1887. They demonstrated experimentally that the velocity of light appears to be the same regardless of the direction it is aimed from a moving source. In this experiment, the velocity of light was measured in reference to Earth’s motion as it orbits the Sun. The instrument used was an interferometer they built on a large slab of sandstone which was floated on a sea of mercury. This made it possible to change the orientation of the instrument and the direction the photons are ejected from their source, and subsequently their direction moving through the interferometer, without disturbing its adjustment. By this means they could compare the velocity of light traveling in various directions. If Earth’s rotation did indeed affect the velocity of the photon, this instrument was easily capable of detecting Earth’s orbital velocity of 29,786 meters per second. The final result of this sensitive experiment indicated that light leaving a source was not influenced by Earth’s rotation as measured in their interferometer.
Of course, this is far different than a bullet short from a moving train. If a bullet is shot in the same direction the train is moving, its velocity is the combined sum of mussel velocity and train velocity; whereas, a bullet shot in the opposite direction is slower because the train’s velocity must be subtracted from mussel velocity. All of this is perfectly reasonable, which caused the scientists at the time to ask why it doesn’t apply to the velocity of light?
The Irish physicist, G. Fitzgerald, suggested that the velocity of light is modified by Earth’s velocity, but cannot be detected in the Michelson-Morley experiment because the length of the instrument (slab of sandstone) shrinks in the direction it is moving. A Dutch physicist by the name of Hendrik Lorentz derived an equation that makes it possible to calculate what the shrinkage would have to be for a given velocity. This article was published in 1892. This equation is known as the Lorentz contraction, and it is always less than one.

Where v is the velocity of the instrument and c is the velocity of light.
Thus, the length of the interferometer would vary according to its velocity with respect to the normal velocity of light as shown in the following equation:

Because the Lorentz contraction is always less than one, the length in motion is always less than the length at rest.
This equation, along with other uses of the Lorentz contraction, forms the basis of the special theory of relativity. I will continue with this discussion in my next blog. Till then be safe and in good health. Kelland—www.vestheory.com
Albert Einstein published his special theory of relativity in 1905. This theory has been used to explain the odd behavior of electrons and radioactive particles in particle accelerators, the strange behavior of atomic clocks and radioactive particles in motion, and other curious phenomenon involving photons. I will come back to these observations after I discuss the origin of the equation that forms the backbone of special relativity.
The theory of relativity has its roots in an experiment carried out by A. Michelson and E. W. Morley in 1887. They demonstrated experimentally that the velocity of light appears to be the same regardless of the direction it is aimed from a moving source. In this experiment, the velocity of light was measured in reference to Earth’s motion as it orbits the Sun. The instrument used was an interferometer they built on a large slab of sandstone which was floated on a sea of mercury. This made it possible to change the orientation of the instrument and the direction the photons are ejected from their source, and subsequently their direction moving through the interferometer, without disturbing its adjustment. By this means they could compare the velocity of light traveling in various directions. If Earth’s rotation did indeed affect the velocity of the photon, this instrument was easily capable of detecting Earth’s orbital velocity of 29,786 meters per second. The final result of this sensitive experiment indicated that light leaving a source was not influenced by Earth’s rotation as measured in their interferometer.
Of course, this is far different than a bullet short from a moving train. If a bullet is shot in the same direction the train is moving, its velocity is the combined sum of mussel velocity and train velocity; whereas, a bullet shot in the opposite direction is slower because the train’s velocity must be subtracted from mussel velocity. All of this is perfectly reasonable, which caused the scientists at the time to ask why it doesn’t apply to the velocity of light?
The Irish physicist, G. Fitzgerald, suggested that the velocity of light is modified by Earth’s velocity, but cannot be detected in the Michelson-Morley experiment because the length of the instrument (slab of sandstone) shrinks in the direction it is moving. A Dutch physicist by the name of Hendrik Lorentz derived an equation that makes it possible to calculate what the shrinkage would have to be for a given velocity. This article was published in 1892. This equation is known as the Lorentz contraction, and it is always less than one.

Where v is the velocity of the instrument and c is the velocity of light.
Thus, the length of the interferometer would vary according to its velocity with respect to the normal velocity of light as shown in the following equation:

Because the Lorentz contraction is always less than one, the length in motion is always less than the length at rest.
This equation, along with other uses of the Lorentz contraction, forms the basis of the special theory of relativity. I will continue with this discussion in my next blog. Till then be safe and in good health. Kelland—www.vestheory.com
Labels:
interferometer,
Michelson-Morley,
speed of light
Monday, February 13, 2012
Normal velocity of photons
The Forces of Nature by Kelland Terry, Ph.D
The balance reached between the photon and a sea of graviton waves traveling in all direction results in a photon with a velocity slightly less than 3 x 10^8 m/s. In contrast an electron in orbit has a velocity of approximately 2 x 10^6 m/s, or even less in the solar wind. There are important differences between photons and electrons that likely explain the difference in their normal velocities even though both are being pushed through space by the same graviton waves.
In contrast to electrons, the two spheres of the photon eject the same string mass per unit time. This means it is always in perfect balance, which allows graviton waves to push it smoothly through space. In addition, the photon has free electons emanating from one sphere, and at the same time, it has an equal mass of free magnons emanating from the other sphere. It seems graviton waves are able to generate more force against free strings than those strings that eventually become bound as complimentary pairs. This would help explain why the normal velocity of photons is higher than the normal velocity of electrons in orbit.
Photons can be as massive as electrons or immensely smaller as in the case of a radio wave photon. Even a photon of visible light can be as much as 10^11 times more massive than a radio wave photon, yet all photons travel at the same velocity even though each makes the same number of strings during the peak of their string cycle. This suggests that an upper limit exists, which holds all photons to the same velocity. This same upper limit also exists for electrons that are forced to travel at high speeds in a particle accelerator. In my next series of blogs, I will begin a discussion of situations where the velocities of electrons and photons are modified by scientists. Till then be safe and in good health. Kelland—www.vestheory.com
The balance reached between the photon and a sea of graviton waves traveling in all direction results in a photon with a velocity slightly less than 3 x 10^8 m/s. In contrast an electron in orbit has a velocity of approximately 2 x 10^6 m/s, or even less in the solar wind. There are important differences between photons and electrons that likely explain the difference in their normal velocities even though both are being pushed through space by the same graviton waves.
In contrast to electrons, the two spheres of the photon eject the same string mass per unit time. This means it is always in perfect balance, which allows graviton waves to push it smoothly through space. In addition, the photon has free electons emanating from one sphere, and at the same time, it has an equal mass of free magnons emanating from the other sphere. It seems graviton waves are able to generate more force against free strings than those strings that eventually become bound as complimentary pairs. This would help explain why the normal velocity of photons is higher than the normal velocity of electrons in orbit.
Photons can be as massive as electrons or immensely smaller as in the case of a radio wave photon. Even a photon of visible light can be as much as 10^11 times more massive than a radio wave photon, yet all photons travel at the same velocity even though each makes the same number of strings during the peak of their string cycle. This suggests that an upper limit exists, which holds all photons to the same velocity. This same upper limit also exists for electrons that are forced to travel at high speeds in a particle accelerator. In my next series of blogs, I will begin a discussion of situations where the velocities of electrons and photons are modified by scientists. Till then be safe and in good health. Kelland—www.vestheory.com
Sunday, February 12, 2012
Normal velocity of the electron
The Forces of Nature by Kelland Terry, Ph.D.
The velocity of the electron in orbit about the proton is 2 x 10^6 m/s. It has the same velocity irrespective of its distance from the proton. This is exactly what we might expect if its velocity is dictated by the balance between opposing graviton waves. In contrast, the velocity of electrons in the solar wind may be as low as 10^5 m/s, yet we must assume both are being driven by graviton waves. I believe the differences can be explained by their orientation in flight.
The electron creates a negative electric field composed of e-electon strings that are not in balance with an equal number of p-electon strings. When the electron is in orbit about the proton, its free e-electons become bound to p-electons emanating from the proton, which allows it to move smoothly through space. Scientists know the electron in orbit only spins either up or down. This suggests that the electron is moving smoothly through space, not tumbling end over end. This is what we might expect if the free e-electons are being created from just one sphere of the electron. This sphere becomes oriented towards the proton when its e-electons become bound to the p-electons emanating from the proton as shown in the following illustration.

Notice, if the electron is coming towards the viewer it only has the option of spinning up or down just as experiments verify.
The electron’s remaining strings are acted upon by graviton waves traveling in both directions, which results in the normal velocity of the electron in orbit. It prevents the electron from spiraling into the proton.
In contrast to this situation, when the electron is moving in the solar wind, its free e-electons cause the electron to be out of balance. One sphere will be acted upon with graviton waves more than the other sphere, which will cause the electron to tumble through space. This will cause the electrons in the solar wind to have less velocity than electrons in orbit about protons.
The velocity of the electron in orbit about the proton is 2 x 10^6 m/s. It has the same velocity irrespective of its distance from the proton. This is exactly what we might expect if its velocity is dictated by the balance between opposing graviton waves. In contrast, the velocity of electrons in the solar wind may be as low as 10^5 m/s, yet we must assume both are being driven by graviton waves. I believe the differences can be explained by their orientation in flight.
The electron creates a negative electric field composed of e-electon strings that are not in balance with an equal number of p-electon strings. When the electron is in orbit about the proton, its free e-electons become bound to p-electons emanating from the proton, which allows it to move smoothly through space. Scientists know the electron in orbit only spins either up or down. This suggests that the electron is moving smoothly through space, not tumbling end over end. This is what we might expect if the free e-electons are being created from just one sphere of the electron. This sphere becomes oriented towards the proton when its e-electons become bound to the p-electons emanating from the proton as shown in the following illustration.

Notice, if the electron is coming towards the viewer it only has the option of spinning up or down just as experiments verify.
The electron’s remaining strings are acted upon by graviton waves traveling in both directions, which results in the normal velocity of the electron in orbit. It prevents the electron from spiraling into the proton.
In contrast to this situation, when the electron is moving in the solar wind, its free e-electons cause the electron to be out of balance. One sphere will be acted upon with graviton waves more than the other sphere, which will cause the electron to tumble through space. This will cause the electrons in the solar wind to have less velocity than electrons in orbit about protons.
Saturday, February 11, 2012
Graviton waves are formidable forces
The Forces of Nature by Kelland Terry, Ph.D.
In a previous discussion, I pointed out that the number of gravitons per unit area may be 10^15 times greater than electons, and 10^25 times greater than magnons. This means there is a sea of graviton waves traveling in all directions that are in intimate contact with the electons and magnons associated with photons and electrons.
In the previous blogs, I assumed the velocity of the graviton waves is 10^23 m/s and magnon and electon waves are 10^15 m/s. Now, if we assume the mass of gravitons in intimate contact with the electons and magnons approaches their mass, then the total momentum of the graviton waves becomes 10^8 times greater than the electon or magnon waves.
These guesstimates suggest that the energy of graviton waves far exceeds that necessary to push either an electron or photon through space.
When the photon is traveling at the speed of light, the large positive force pushing the photon through space is slightly greater than the large negative force. In the case of the electron, the positive forces are slightly greater than the negative forces when the electron is traveling at 2 x 10^6 m/s. At this point, negative and positive forces are at equilibrium. To increase the velocity of the electron higher than 2 x 10^6 requires an outside source of energy.
The great opposing graviton wave forces helps to explain why a small increase in electron velocity meets with great resistance.
In a previous discussion, I pointed out that the number of gravitons per unit area may be 10^15 times greater than electons, and 10^25 times greater than magnons. This means there is a sea of graviton waves traveling in all directions that are in intimate contact with the electons and magnons associated with photons and electrons.
In the previous blogs, I assumed the velocity of the graviton waves is 10^23 m/s and magnon and electon waves are 10^15 m/s. Now, if we assume the mass of gravitons in intimate contact with the electons and magnons approaches their mass, then the total momentum of the graviton waves becomes 10^8 times greater than the electon or magnon waves.
These guesstimates suggest that the energy of graviton waves far exceeds that necessary to push either an electron or photon through space.
When the photon is traveling at the speed of light, the large positive force pushing the photon through space is slightly greater than the large negative force. In the case of the electron, the positive forces are slightly greater than the negative forces when the electron is traveling at 2 x 10^6 m/s. At this point, negative and positive forces are at equilibrium. To increase the velocity of the electron higher than 2 x 10^6 requires an outside source of energy.
The great opposing graviton wave forces helps to explain why a small increase in electron velocity meets with great resistance.
Friday, February 10, 2012
Velocity of magnon and electon waves
The Forces of Nature by Kelland Terry, Ph.D.
In the previous blog, I assumed for the reasons given that graviton waves travel along the string at 10^23 meters per second. An analysis of the equation that computes wave velocity tells us that the velocity of magnon and electon waves is much less than graviton waves.

This is true because the theory holds that electons and magnons have much greater masses than gravitons, and their masses are spread over a relatively short distance in space, not across galaxies as is the case for gravitons. This means kg/m is much higher for electons and magnons, which will make their wave speed much slower. This is an important point because my model dictates that the velocity of graviton waves is greater than electon and magnon waves.
Because photons eject the same mass of electons and magnons with every string cycle, it suggests they are ejected the same distance in space. This means electons and magnons would have the same wave velocity. I refer you to the equation given for wave velocity. If the restoring force F for a magnon is 10^8 times greater than the restoring force of an electon, and if its mass is 10^8 greater per km, the equation dictates that the waves have the same velocity. I guesstimate the speed of these waves at 10^15 meters/second, which I will discuss in a future blog.
The negative and positive graviton wave forces are much greater than necessary to push electrons and photons through space. I will discuss this in my next blog. Till then be safe and in good health. Kelland—www.vestheory.com
In the previous blog, I assumed for the reasons given that graviton waves travel along the string at 10^23 meters per second. An analysis of the equation that computes wave velocity tells us that the velocity of magnon and electon waves is much less than graviton waves.

This is true because the theory holds that electons and magnons have much greater masses than gravitons, and their masses are spread over a relatively short distance in space, not across galaxies as is the case for gravitons. This means kg/m is much higher for electons and magnons, which will make their wave speed much slower. This is an important point because my model dictates that the velocity of graviton waves is greater than electon and magnon waves.
Because photons eject the same mass of electons and magnons with every string cycle, it suggests they are ejected the same distance in space. This means electons and magnons would have the same wave velocity. I refer you to the equation given for wave velocity. If the restoring force F for a magnon is 10^8 times greater than the restoring force of an electon, and if its mass is 10^8 greater per km, the equation dictates that the waves have the same velocity. I guesstimate the speed of these waves at 10^15 meters/second, which I will discuss in a future blog.
The negative and positive graviton wave forces are much greater than necessary to push electrons and photons through space. I will discuss this in my next blog. Till then be safe and in good health. Kelland—www.vestheory.com
Thursday, February 9, 2012
Velocity of graviton waves
The Forces of Nature by Kelland Terry, Ph.D.
The relative velocity of the electon and magnon waves verses graviton waves is central to understanding relativity. Although it isn’t necessary to know their absolute velocities, a guesstimate eases discussion.
There are two lines of reasoning that convince me that graviton waves travel at enormous velocity. First, my ether model requires that the velocity of graviton waves has to be almost as great as the speed of the graviton as it is generated into space (10^23 m/s). Why this must be true comes from the observation that stars in our local cluster of galaxies influence the photons they emit for their entire journey to Earth. For example, the Andromeda galaxy is 2.5 million light years away (about 2 x 10^22 meters), and the light we receive from this galaxy has higher energy than expected.
If the blue shift is created by gravitons emanating from Andromeda, then graviton waves must travel at least 2 x 10^22 meters before the graviton is retracted. Even if the graviton existed for one full second, the waves would have to travel more than 2 x 10^22 meters per second.
There is another line of reasoning that supports the idea that graviton waves travel at very high velocity. This comes from the equation provided by physicists that explains the velocity of waves along a common string.

In this equation, F is the restoring force that snaps the string back in place. It is also the force conducted along the string. It is expressed in newtons. Two other elements used in the equation are mass per unit length (kg/m) and the velocity of the waves in meters per second. Notice, if the mass of the string is extremely small, especially when expressed as kg/meter, then wave speed must be extremely large. The mass of a graviton might be as little as 10^80 kg, which would mean its mass per meter might be as little as 10^103 kg. This explains why the speed of the wave traveling along the string has great velocity.
This equation holds if the amplitude of the wave is small. This is certainly true for waves contemplated here because they are nothing more than tiny pulses created by snapping portals.
For sake of argument, I will assume that graviton waves travel along the string at 10^23 m/s.
I will come back to the mass of gravitons and the other strings in a future blog.
In my next blog, I will take up the velocity of magnon and electon waves. Till then be safe and in good health. Kelland—www.vestheory.com
The relative velocity of the electon and magnon waves verses graviton waves is central to understanding relativity. Although it isn’t necessary to know their absolute velocities, a guesstimate eases discussion.
There are two lines of reasoning that convince me that graviton waves travel at enormous velocity. First, my ether model requires that the velocity of graviton waves has to be almost as great as the speed of the graviton as it is generated into space (10^23 m/s). Why this must be true comes from the observation that stars in our local cluster of galaxies influence the photons they emit for their entire journey to Earth. For example, the Andromeda galaxy is 2.5 million light years away (about 2 x 10^22 meters), and the light we receive from this galaxy has higher energy than expected.
If the blue shift is created by gravitons emanating from Andromeda, then graviton waves must travel at least 2 x 10^22 meters before the graviton is retracted. Even if the graviton existed for one full second, the waves would have to travel more than 2 x 10^22 meters per second.
There is another line of reasoning that supports the idea that graviton waves travel at very high velocity. This comes from the equation provided by physicists that explains the velocity of waves along a common string.

In this equation, F is the restoring force that snaps the string back in place. It is also the force conducted along the string. It is expressed in newtons. Two other elements used in the equation are mass per unit length (kg/m) and the velocity of the waves in meters per second. Notice, if the mass of the string is extremely small, especially when expressed as kg/meter, then wave speed must be extremely large. The mass of a graviton might be as little as 10^80 kg, which would mean its mass per meter might be as little as 10^103 kg. This explains why the speed of the wave traveling along the string has great velocity.
This equation holds if the amplitude of the wave is small. This is certainly true for waves contemplated here because they are nothing more than tiny pulses created by snapping portals.
For sake of argument, I will assume that graviton waves travel along the string at 10^23 m/s.
I will come back to the mass of gravitons and the other strings in a future blog.
In my next blog, I will take up the velocity of magnon and electon waves. Till then be safe and in good health. Kelland—www.vestheory.com
Wednesday, February 8, 2012
Graviton waves nudge electrons and photons forward in flight
The Forces of Nature by Kelland Terry, Ph.D.
VES ether theory is based on the idea that a sea of graviton waves transfers energy to photons and electrons, which modulates their velocity. The following are a few reasons why an energy source is needed to explain the flight of electrons and photons.
• The velocity of a photon always tends to be 299,792,459 m/s even though it ejects virtual particles at right angles to its line of flight as it plows through a dense matrix of gravitons in its path. One would think it should slow down under these conditions but it does not.
• The velocity of a photon tends to be constant even when propelled from a moving source such as in the Michelson-Morley experiment. This suggests an energy source exists in the ether that instantly changes its velocity.
• The velocity of the electron in orbit is always the same even though its circular pathway is at various distances from the proton. Its velocity is 2 x 10^6 m/s.
• An electron never loses velocity and spirals into the nucleus.
• Two lines of experiments suggest that light can be made to slow down a tad if moving against a strong field of graviton waves.
We know from Maxwell’s equations that the strength of the electric field divided by the strength of the magnetic field equals the velocity of light:

This means gravitons have their effect on velocity by pushing on electron and photon string waves.
I previously illustrated how graviton waves push electrons and photons through space. A little review doesn’t hurt.

When graviton waves are traveling in the same direction as the electron or photon, they crash into the electon and magnon waves coming towards them. This causes them to rebound away from each other because they have perfect elasticity. My drawing dramatizes the results for sake of clarity. As the magnon and electon waves rebound, they push on the electron or photon they are bound to.
Of course this is not the whole story. Graviton waves traveling in one direction are always in competition with waves going in the opposite direction as previously discussed.
Graviton waves traveling in the opposite direction to the electron or photons flight path have a negative effect on particle velocity and a negative effect on string cycles. In actuality they are traveling in the same direction as the magnon and electon waves.

Graviton waves traveling in the same direction as the magnon and electon waves nudge these waves to the rear of the electron, which decreases the velocity of the electron and its string cycles. However, the wave fronts are at a disadvantage compared to the situation where the graviton waves are going in the opposite direction because of the orientation of their wave fronts. This helps to explain why those gravitons going in the same direction as the electron or photon have the greatest influence on electron or photon velocity.
The dynamics between graviton waves is very sensitive as the particle approaches the speed of light. Because the opposing graviton waves are large forces, any interruption in this equilibrium can cause a dramatic effect on the velocity and string cycles of these particles. I will come back to this point when I discuss the special theory of relativity. Kelland—www.vestheory.com
VES ether theory is based on the idea that a sea of graviton waves transfers energy to photons and electrons, which modulates their velocity. The following are a few reasons why an energy source is needed to explain the flight of electrons and photons.
• The velocity of a photon always tends to be 299,792,459 m/s even though it ejects virtual particles at right angles to its line of flight as it plows through a dense matrix of gravitons in its path. One would think it should slow down under these conditions but it does not.
• The velocity of a photon tends to be constant even when propelled from a moving source such as in the Michelson-Morley experiment. This suggests an energy source exists in the ether that instantly changes its velocity.
• The velocity of the electron in orbit is always the same even though its circular pathway is at various distances from the proton. Its velocity is 2 x 10^6 m/s.
• An electron never loses velocity and spirals into the nucleus.
• Two lines of experiments suggest that light can be made to slow down a tad if moving against a strong field of graviton waves.
We know from Maxwell’s equations that the strength of the electric field divided by the strength of the magnetic field equals the velocity of light:

This means gravitons have their effect on velocity by pushing on electron and photon string waves.
I previously illustrated how graviton waves push electrons and photons through space. A little review doesn’t hurt.

When graviton waves are traveling in the same direction as the electron or photon, they crash into the electon and magnon waves coming towards them. This causes them to rebound away from each other because they have perfect elasticity. My drawing dramatizes the results for sake of clarity. As the magnon and electon waves rebound, they push on the electron or photon they are bound to.
Of course this is not the whole story. Graviton waves traveling in one direction are always in competition with waves going in the opposite direction as previously discussed.
Graviton waves traveling in the opposite direction to the electron or photons flight path have a negative effect on particle velocity and a negative effect on string cycles. In actuality they are traveling in the same direction as the magnon and electon waves.

Graviton waves traveling in the same direction as the magnon and electon waves nudge these waves to the rear of the electron, which decreases the velocity of the electron and its string cycles. However, the wave fronts are at a disadvantage compared to the situation where the graviton waves are going in the opposite direction because of the orientation of their wave fronts. This helps to explain why those gravitons going in the same direction as the electron or photon have the greatest influence on electron or photon velocity.
The dynamics between graviton waves is very sensitive as the particle approaches the speed of light. Because the opposing graviton waves are large forces, any interruption in this equilibrium can cause a dramatic effect on the velocity and string cycles of these particles. I will come back to this point when I discuss the special theory of relativity. Kelland—www.vestheory.com
Tuesday, February 7, 2012
Decay Rate of Radioactive Particles
The Forces of Nature by Kelland Terry, Ph.D.
Physicists have shown that the decay rate of radioactive particles is slower when Earth is closer to the Sun. They do not believe the seasonal variation in decay rate is determined by a fluctuation in temperature, for example; rather they believe it is determined by some field of the Sun.
According to VES ether theory, this field is composed of gravitons whose concentration increases the closer we are to the Sun. An increasing concentration of gravitons lowers string cycle rate and decreases the energy of the particle, which in turn decreases the rate of decay.
Once more we find evidence that gravitons influence string cycles and the energy of atoms. Gravitational frequency shift, gravitational red shift, and radioactive decay rate all show that string cycle rates decrease in stronger gravitational fields even if the number of graviton waves is equal in all directions. Those graviton waves traveling opposite to the flightpath of the electron or photon cause this effect, although it must be remembered that the final rate of the string cycle depends on the dynamics between graviton waves traveling in both directions.
In my next series of blogs, I will explain how gravitons affect the velocity of electrons and photons. Kelland—www.vestheory.com
Physicists have shown that the decay rate of radioactive particles is slower when Earth is closer to the Sun. They do not believe the seasonal variation in decay rate is determined by a fluctuation in temperature, for example; rather they believe it is determined by some field of the Sun.
According to VES ether theory, this field is composed of gravitons whose concentration increases the closer we are to the Sun. An increasing concentration of gravitons lowers string cycle rate and decreases the energy of the particle, which in turn decreases the rate of decay.
Once more we find evidence that gravitons influence string cycles and the energy of atoms. Gravitational frequency shift, gravitational red shift, and radioactive decay rate all show that string cycle rates decrease in stronger gravitational fields even if the number of graviton waves is equal in all directions. Those graviton waves traveling opposite to the flightpath of the electron or photon cause this effect, although it must be remembered that the final rate of the string cycle depends on the dynamics between graviton waves traveling in both directions.
In my next series of blogs, I will explain how gravitons affect the velocity of electrons and photons. Kelland—www.vestheory.com
Monday, February 6, 2012
Gravitational red shift
The Forces of Nature by Kelland Terry, Ph.D.
In the previous section, I explained how atoms in a strong gravitational field have a slower than normal vibration frequency because their string cycles are extended. As we might expect, this affects the photons emitted by these atoms.
All atoms have a different number of electrons orbiting about their nuclei as well as a different number of protons and neutrons, and the photons they emit when in an exited state are characteristic for that particular atom. This provides a method of identifying different elements by their spectral lines, their “cosmic bar code”.
Photons emitted by atoms in a strong gravitational field have lower frequencies than expected; their bar codes have been shifted. This is referred to as a red shift because red is found at the lower end of the light spectrum. It was first measured in the light we receive from massive stars called white dwarfs. It is frequently offered as proof for the general theory of relativity. As the name implies, the gravitational red shift is known by scientists to be the result of strong gravitational fields.
Physicists have known for many years that the rate atoms oscillate influences the photons emitted. This enabled Max Planck to establish the relationship between the oscillation of atoms and the oscillation frequency of the photon’s emitted by these atoms.
Electricity is used to control the energy of the photons emitted by a transmitting radio antenna. It is used to modify the oscillation frequency of the atoms in the antenna, and in this manner, control the frequency of the radio waves emitted.
According to VES theory when graviton waves slow down the rate of oscillation, it decreases the spin angular momentum of the atom’s quarks and electrons, and this causes the atom to make a photon with less energy; it will show a red shift.
The photons emitted by atoms in a strong gravitational field have lower frequencies because the atoms that emit the photons have slower string cycles.
Elastic string theory explains the connection between the gravitational red shift and the gravitational frequency shift. Kelland—www.vestheory.com
In the previous section, I explained how atoms in a strong gravitational field have a slower than normal vibration frequency because their string cycles are extended. As we might expect, this affects the photons emitted by these atoms.
All atoms have a different number of electrons orbiting about their nuclei as well as a different number of protons and neutrons, and the photons they emit when in an exited state are characteristic for that particular atom. This provides a method of identifying different elements by their spectral lines, their “cosmic bar code”.
Photons emitted by atoms in a strong gravitational field have lower frequencies than expected; their bar codes have been shifted. This is referred to as a red shift because red is found at the lower end of the light spectrum. It was first measured in the light we receive from massive stars called white dwarfs. It is frequently offered as proof for the general theory of relativity. As the name implies, the gravitational red shift is known by scientists to be the result of strong gravitational fields.
Physicists have known for many years that the rate atoms oscillate influences the photons emitted. This enabled Max Planck to establish the relationship between the oscillation of atoms and the oscillation frequency of the photon’s emitted by these atoms.
Electricity is used to control the energy of the photons emitted by a transmitting radio antenna. It is used to modify the oscillation frequency of the atoms in the antenna, and in this manner, control the frequency of the radio waves emitted.
According to VES theory when graviton waves slow down the rate of oscillation, it decreases the spin angular momentum of the atom’s quarks and electrons, and this causes the atom to make a photon with less energy; it will show a red shift.
The photons emitted by atoms in a strong gravitational field have lower frequencies because the atoms that emit the photons have slower string cycles.
Elastic string theory explains the connection between the gravitational red shift and the gravitational frequency shift. Kelland—www.vestheory.com
Sunday, February 5, 2012
Frequency shift and earth’s potential gravitational energy
The Forces of Nature by Kelland Terry, Ph.D.
Scientists have shown that the magnitude of the gravitational frequency shift is directly related to Earth’s potential gravitational energy.

Where G is the gravitational constant, ME the mass of the Earth, and r is the distance to Earth’s center.
According to VES ether theory, Earth’s potential gravitational energy at a given distance from Earth reflects the concentration of gravitons in the area. It provides a rational, physical reason why the strength of the gravitational field is correlated with the rate atoms vibrate.
The very fact that Earth’s potential gravitational energy is used to calculate the gravitational frequency shift gives strong support to the idea that gravitons interact with electons and magnons just as predicted to explain the gravitational frequency shift.
By the way, no theory of relativity is required to calculate Earth’s potential gravitational energy. Kelland—www.vestheory.com
Scientists have shown that the magnitude of the gravitational frequency shift is directly related to Earth’s potential gravitational energy.

Where G is the gravitational constant, ME the mass of the Earth, and r is the distance to Earth’s center.
According to VES ether theory, Earth’s potential gravitational energy at a given distance from Earth reflects the concentration of gravitons in the area. It provides a rational, physical reason why the strength of the gravitational field is correlated with the rate atoms vibrate.
The very fact that Earth’s potential gravitational energy is used to calculate the gravitational frequency shift gives strong support to the idea that gravitons interact with electons and magnons just as predicted to explain the gravitational frequency shift.
By the way, no theory of relativity is required to calculate Earth’s potential gravitational energy. Kelland—www.vestheory.com
Saturday, February 4, 2012
The gravitational frequency shift: Atomic clocks slow down in strong gravitational fields
The Forces of Nature by Kelland Terry, Ph.D.
A cesium-beam atomic clock measures the exact oscillation frequency of the cesium atom, which is 9,192,631,770 cycles/second. This amounts to an accuracy of 1 second in 1,400,000 years, which makes a cesium-beam atomic clock the most sensitive device ever made for measuring time.
The oscillation frequency of an atom is determined by its string cycles. Electron string cycles and quark string cycles become synchronized because their e-electons and p-electons bond as they go through their individual cycles. This forces them into synchrony.
It has been shown that a cesium clock slows down when placed in a stronger gravitational field. This is referred to as the gravitational frequency shift. Clocks here on Earth run slower at lower altitudes where the gravitational force is greater. Even a clock placed at the bottom of a skyscraper runs slower than a clock at the top of the skyscraper. Physicists have shown that clocks in the Northern Hemisphere during the winter, when closer to the Sun, run slower than clocks at the same location during the summer. Atomic clocks aboard satellites must be corrected for the gravitational frequency shift; otherwise, the lower density of gravitons in outer space would cause the clocks to run faster. The correction is only one part in 10^14.
According to VES ether theory, a greater concentration of gravitons will slow down string retraction and increase the length of string cycles. The net result is an atom whose electron string cycles and quark string cycles are in synchrony but at a lower frequency. The clock will have a slower oscillation frequency and tick fewer times per second. This completely explains the effect of the gravitational force on cesium-beam clocks. It provides strong evidence that gravitons influence string cycle rates.
It can be shown mathematically that the gravitational frequency shift is directly correlated with the concentration of gravitons in the area. I will continue with this discussion in my next blog. Kelland—www.vestheory.com
A cesium-beam atomic clock measures the exact oscillation frequency of the cesium atom, which is 9,192,631,770 cycles/second. This amounts to an accuracy of 1 second in 1,400,000 years, which makes a cesium-beam atomic clock the most sensitive device ever made for measuring time.
The oscillation frequency of an atom is determined by its string cycles. Electron string cycles and quark string cycles become synchronized because their e-electons and p-electons bond as they go through their individual cycles. This forces them into synchrony.
It has been shown that a cesium clock slows down when placed in a stronger gravitational field. This is referred to as the gravitational frequency shift. Clocks here on Earth run slower at lower altitudes where the gravitational force is greater. Even a clock placed at the bottom of a skyscraper runs slower than a clock at the top of the skyscraper. Physicists have shown that clocks in the Northern Hemisphere during the winter, when closer to the Sun, run slower than clocks at the same location during the summer. Atomic clocks aboard satellites must be corrected for the gravitational frequency shift; otherwise, the lower density of gravitons in outer space would cause the clocks to run faster. The correction is only one part in 10^14.
According to VES ether theory, a greater concentration of gravitons will slow down string retraction and increase the length of string cycles. The net result is an atom whose electron string cycles and quark string cycles are in synchrony but at a lower frequency. The clock will have a slower oscillation frequency and tick fewer times per second. This completely explains the effect of the gravitational force on cesium-beam clocks. It provides strong evidence that gravitons influence string cycle rates.
It can be shown mathematically that the gravitational frequency shift is directly correlated with the concentration of gravitons in the area. I will continue with this discussion in my next blog. Kelland—www.vestheory.com
Friday, February 3, 2012
The influence of graviton waves on string cycles
The Forces of Nature by Kelland Terry, Ph.D.
Electons and magnons emanating from electrons and photons have perfect elasticity, which enables them to retract back to their source. However, a sea of graviton waves in physical contact with these strings influence their rate of retraction and string cycles.
• Graviton waves traveling in the same direction as the magnon waves and electons waves push these waves to the rear away from the particle. This inhibits their retraction and increases the length of the string cycle.

• Gravitons waves traveling against the flow of the electon and magnon waves tend to decrease the string cycle because they push these waves towards the photon or electron. However, they have less influence on string cycles than graviton waves going in the opposite direction. This is born out by the facts.

• The evidence shows that string cycle rates decrease in stronger gravitational fields even if the number of waves is equal in all directions.
• When there is a preponderance of graviton waves going in one direction, the balance shifts. I will take this up in future blogs.
In my next blog, I will take a closer look at gravitational fields and how they affect Cesium based atomic clocks.
Electons and magnons emanating from electrons and photons have perfect elasticity, which enables them to retract back to their source. However, a sea of graviton waves in physical contact with these strings influence their rate of retraction and string cycles.
• Graviton waves traveling in the same direction as the magnon waves and electons waves push these waves to the rear away from the particle. This inhibits their retraction and increases the length of the string cycle.

• Gravitons waves traveling against the flow of the electon and magnon waves tend to decrease the string cycle because they push these waves towards the photon or electron. However, they have less influence on string cycles than graviton waves going in the opposite direction. This is born out by the facts.

• The evidence shows that string cycle rates decrease in stronger gravitational fields even if the number of waves is equal in all directions.
• When there is a preponderance of graviton waves going in one direction, the balance shifts. I will take this up in future blogs.
In my next blog, I will take a closer look at gravitational fields and how they affect Cesium based atomic clocks.
Thursday, February 2, 2012
Collision between particles with perfect elasticity
The Forces of Nature by Kelland Terry, Ph.D.
When two balls with perfect elasticity collide head on, they reverse directions and bound away from each other with the same velocity and momentum they had before the collision.

And for the same reason, if a faster moving ball collides with a slower ball going in the same direction, momentum will be transferred to the slow ball causing it to travel faster; however, there will be no change in total momentum because the two balls have perfect elasticity.

In the case of string waves, the interaction between waves depends on their orientation in space and wave direction. If the waves are traveling in the opposite direction, the broad fronts of the waves might crash into each other as shown.

Because the waves have perfect elasticity, the magnon and electon waves will tend to reverse direction, which will shorten the string cycle and increase the velocity of the particle.
On the other hand if the waves are traveling in the same direction, one possible orientation might be as shown.

In this situation, the graviton wave is nudging the electon wave to the rear, which will decrease photon velocity and decrease string cycle rate. It seems likely that the collision between waves in this situation will result in less force per collision than when the waves are going in the opposite direction because of the nature of the wave fronts.
The actual velocity of the photon and its string cycle rate will depend upon the overall dynamics between waves, and when the concentration of graviton waves is equal in both directions, the photon or electron reaches its normal velocity and its normal string cycle.
I will first examine how graviton waves influence string cycles. Till then be safe and in good health. Kelland—www.vestheory.com
When two balls with perfect elasticity collide head on, they reverse directions and bound away from each other with the same velocity and momentum they had before the collision.

And for the same reason, if a faster moving ball collides with a slower ball going in the same direction, momentum will be transferred to the slow ball causing it to travel faster; however, there will be no change in total momentum because the two balls have perfect elasticity.

In the case of string waves, the interaction between waves depends on their orientation in space and wave direction. If the waves are traveling in the opposite direction, the broad fronts of the waves might crash into each other as shown.

Because the waves have perfect elasticity, the magnon and electon waves will tend to reverse direction, which will shorten the string cycle and increase the velocity of the particle.
On the other hand if the waves are traveling in the same direction, one possible orientation might be as shown.

In this situation, the graviton wave is nudging the electon wave to the rear, which will decrease photon velocity and decrease string cycle rate. It seems likely that the collision between waves in this situation will result in less force per collision than when the waves are going in the opposite direction because of the nature of the wave fronts.
The actual velocity of the photon and its string cycle rate will depend upon the overall dynamics between waves, and when the concentration of graviton waves is equal in both directions, the photon or electron reaches its normal velocity and its normal string cycle.
I will first examine how graviton waves influence string cycles. Till then be safe and in good health. Kelland—www.vestheory.com
Wednesday, February 1, 2012
Direction of waves important
The Forces of Nature by Kelland Terry, Ph.D.
A sea of graviton waves is composed of a vast number of waves traveling in all directions; however, only those waves traveling directly with or directly opposed to the orientation of the photon’s strings have an appreciable effect on the photon’s velocity or its string cycle rate.
Electons and magnons are ejected from photons at right angles to their direction of flight and at right angles to each other. Initially, the interaction of graviton waves going with and against the photon’s string waves mainly affect string cycles, not velocity, because the photon’s strings are not in alignment with the photon’s flight path.

Not pictured are photon string waves ejected at 90 degrees angle to the flight of the photon and 90 degrees angle to the string shown, but the situation is the same.
As the photon continues through a maze of strings in their path, the electons and magnons are swept to the rear. This allows complementary strings to meet and bond. Thus, soon after the ejection of a virtual particle a portion of the photon’s strings are directed to the rear.

At this point in time, graviton waves are influencing the velocity of the particle and its string cycle.
Because the string cycle of the electron is so short, it seems likely that during the final stage of the cycle the length of the string oriented directly to the rear must be very short. Even so this phase of the cycle might contribute the most to the velocity of the photon or electron because now all the graviton waves are directly in line with the photon’s flight path.

Graviton waves have to interact with strings that eventual bond or have bonded as complementary strings; otherwise, they would not be able to contribute to the electron’s velocity in orbit because the only free strings, the e-electons, become bound to p-electons emanating from the proton.
What is said here about the interaction of photon string waves and graviton string waves applies equally well with the interaction between graviton waves and electron string waves. However, there are differences between the two particles as discussed in future blogs.
In my next blog, I will examine what we can expect when dealing with a substance with perfect elasticity. Till then be safe and in good health. Kelland—www.vestheory.com
A sea of graviton waves is composed of a vast number of waves traveling in all directions; however, only those waves traveling directly with or directly opposed to the orientation of the photon’s strings have an appreciable effect on the photon’s velocity or its string cycle rate.
Electons and magnons are ejected from photons at right angles to their direction of flight and at right angles to each other. Initially, the interaction of graviton waves going with and against the photon’s string waves mainly affect string cycles, not velocity, because the photon’s strings are not in alignment with the photon’s flight path.

Not pictured are photon string waves ejected at 90 degrees angle to the flight of the photon and 90 degrees angle to the string shown, but the situation is the same.
As the photon continues through a maze of strings in their path, the electons and magnons are swept to the rear. This allows complementary strings to meet and bond. Thus, soon after the ejection of a virtual particle a portion of the photon’s strings are directed to the rear.

At this point in time, graviton waves are influencing the velocity of the particle and its string cycle.
Because the string cycle of the electron is so short, it seems likely that during the final stage of the cycle the length of the string oriented directly to the rear must be very short. Even so this phase of the cycle might contribute the most to the velocity of the photon or electron because now all the graviton waves are directly in line with the photon’s flight path.

Graviton waves have to interact with strings that eventual bond or have bonded as complementary strings; otherwise, they would not be able to contribute to the electron’s velocity in orbit because the only free strings, the e-electons, become bound to p-electons emanating from the proton.
What is said here about the interaction of photon string waves and graviton string waves applies equally well with the interaction between graviton waves and electron string waves. However, there are differences between the two particles as discussed in future blogs.
In my next blog, I will examine what we can expect when dealing with a substance with perfect elasticity. Till then be safe and in good health. Kelland—www.vestheory.com
Subscribe to:
Comments (Atom)