The Forces of Nature by Kelland Terry, Ph.D.
As explained in the previous blog, it requires more energy than expected to accelerate an electron in a particle accelerator. This is particularly true the closer the particle comes to the speed of light. How does VES ether theory solve this puzzle?
First, only those gravitons traveling along the surface of Earth will have an appreciable affect on the particle in the accelerator because those emanating from the ground beneath the accelerator will strike the particle’s waves at 90 degrees to its line of flight or at some other sharp angle. Earth’s gravitons will have far less impact on electron velocity compared to those traveling parallel to the surface of Earth and in line with the accelerator. For this reason, we can assume that an equal number of graviton waves are traveling with and against the subatomic particle being accelerated.
I invite you to go to my blog of 2/2/12 if you choose to review what to expect when balls or waves with perfect elasticity strike each other.
Graviton waves traveling against the flight path of the particle act as negative forces because they impede string retraction and they impede the flight of the electron. At the same time, those waves going in the same direction as the electron in flight act as positive forces. They are the strings responsible for pushing the electron through space, and they tend to increase the rate of string cycles.
The dynamics between these two opposing forces are responsible for normal velocity of electrons in orbit, which is 2 x 10^6 meters per second. However, the dynamics between the forces change dramatically as the electron is forced to travel at the speed of light. I will continue with this discussion in my next blog. Till then be safe and in good health. Kelland—www.vestheory.com
Monday, February 20, 2012
Thursday, February 16, 2012
Electrons in particle accelerators
The Forces of Nature by Kelland Terry, Ph.D.
The velocity of an electron in orbit is 2 x 10^6 meters per second, and somewhat less in the solar wind. To increase the velocity of these particles beyond this point requires a source of energy. This has been examined in particle accelerators.
It has been proven that the acceleration of the electron requires more energy than expected. It is as if the mass of the particle increases as it approaches the speed of light; however, the mass remains the same.
Relative momentum = (gamma) x mass x velocity
Gamma is the reciprocal of the Lorentz factor as previously discussed, and it is always greater than one, which means “relative” momentum is always greater than mass x velocity.

Gamma reflects the additional energy required to raise the electron to a specified velocity. It is a measure of the resistance met by the electron as it is accelerated. In this equation, v is the velocity of the electron in the accelerator and c is the velocity of light. Gamma increases dramatically as the speed of light is approached. This is shown in the next illustration.
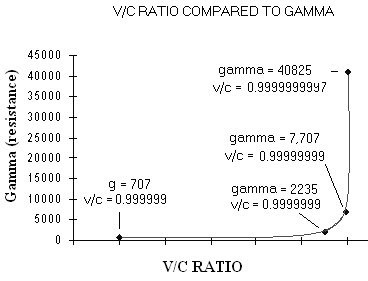
In this illustration, V/C is the ratio of the observed velocity V divided by the velocity of light, C.
As gamma increases from 707 to 40,825 (57.7 fold increase), the velocity of the electron only increases 1.000000999701 fold. Obviously, if the velocity of the electron had increased according to the energy applied, its velocity would have been 57.7 fold greater. This didn’t happen because increasing the velocity of the electron meets with great resistance.
If we live in a three-dimensional world, the question becomes: What is the source of resistance that must be overcome to increase the velocity of the electron? This question can be answered using elastic string theory. Till then be safe and in good health. Kelland—www.vestheory.com
The velocity of an electron in orbit is 2 x 10^6 meters per second, and somewhat less in the solar wind. To increase the velocity of these particles beyond this point requires a source of energy. This has been examined in particle accelerators.
It has been proven that the acceleration of the electron requires more energy than expected. It is as if the mass of the particle increases as it approaches the speed of light; however, the mass remains the same.
Relative momentum = (gamma) x mass x velocity
Gamma is the reciprocal of the Lorentz factor as previously discussed, and it is always greater than one, which means “relative” momentum is always greater than mass x velocity.

Gamma reflects the additional energy required to raise the electron to a specified velocity. It is a measure of the resistance met by the electron as it is accelerated. In this equation, v is the velocity of the electron in the accelerator and c is the velocity of light. Gamma increases dramatically as the speed of light is approached. This is shown in the next illustration.

In this illustration, V/C is the ratio of the observed velocity V divided by the velocity of light, C.
As gamma increases from 707 to 40,825 (57.7 fold increase), the velocity of the electron only increases 1.000000999701 fold. Obviously, if the velocity of the electron had increased according to the energy applied, its velocity would have been 57.7 fold greater. This didn’t happen because increasing the velocity of the electron meets with great resistance.
If we live in a three-dimensional world, the question becomes: What is the source of resistance that must be overcome to increase the velocity of the electron? This question can be answered using elastic string theory. Till then be safe and in good health. Kelland—www.vestheory.com
Wednesday, February 15, 2012
Basic equations used by the special theory of relativity
The Forces of Nature by Kelland Terry, Ph.D.
The special theory of relativity states that time slows down for an object in motion. This means that a clock in motion will actually tick fewer times per second compared to a stationary reference clock because length between ticks is greater. This is spoken of as time dilation. Einstein used the Lorenz equation to define this belief in the following way:
Time dilation
Relativistic time = normal time x gamma.
Where gamma is the inverse of the Lorentz contraction:

Because gamma is always greater than one, relativistic time is always greater than normal time. I will return to this equation when I discuss objects in motion in another section.
Relativistic momentum
The energy required to increase the velocity of an electron to the speed of light is much greater than expected. At one time it was thought that the mass of the particle increased, but this is no longer thought to be the case. The resistance to any increase in the speed of the particle follows gamma.
The special theory of relativity views this as an increase in momentum, which is calculated as follows:
Relativistic momentum = gamma x velocity x mass
This equation actually tells us that it requires more energy than expected to increase the velocity of the electon in a particle accelerator, not that the mass changes. I will return to this equation when I discuss particle accelerators.
Einstein reasoned that these equations can only apply if we live in a four dimensional world rather than the normal three: length, depth, and height. The forth dimension is time, which explains time dilation and the effect of motion on time and particles in motion.
According to relativity theory, the original concept of the Lorentz contraction still applies, although they prefer to state that space shrinks:

This theory does lead to the curious assertion that a large particle accelerator in use shrinks to a few meters.
Is there another way of explaining the odd behavior of particles in motion without invoking a four dimensional world? I believe so. I will begin to tackle this subject in my next blog. Till then be safe and in good health. Kelland—www.vestheory.com
The special theory of relativity states that time slows down for an object in motion. This means that a clock in motion will actually tick fewer times per second compared to a stationary reference clock because length between ticks is greater. This is spoken of as time dilation. Einstein used the Lorenz equation to define this belief in the following way:
Time dilation
Relativistic time = normal time x gamma.
Where gamma is the inverse of the Lorentz contraction:

Because gamma is always greater than one, relativistic time is always greater than normal time. I will return to this equation when I discuss objects in motion in another section.
Relativistic momentum
The energy required to increase the velocity of an electron to the speed of light is much greater than expected. At one time it was thought that the mass of the particle increased, but this is no longer thought to be the case. The resistance to any increase in the speed of the particle follows gamma.
The special theory of relativity views this as an increase in momentum, which is calculated as follows:
Relativistic momentum = gamma x velocity x mass
This equation actually tells us that it requires more energy than expected to increase the velocity of the electon in a particle accelerator, not that the mass changes. I will return to this equation when I discuss particle accelerators.
Einstein reasoned that these equations can only apply if we live in a four dimensional world rather than the normal three: length, depth, and height. The forth dimension is time, which explains time dilation and the effect of motion on time and particles in motion.
According to relativity theory, the original concept of the Lorentz contraction still applies, although they prefer to state that space shrinks:

This theory does lead to the curious assertion that a large particle accelerator in use shrinks to a few meters.
Is there another way of explaining the odd behavior of particles in motion without invoking a four dimensional world? I believe so. I will begin to tackle this subject in my next blog. Till then be safe and in good health. Kelland—www.vestheory.com
Tuesday, February 14, 2012
The Michelson-Morley Experiment
The Forces of Nature by Kelland Terry, Ph.D.
Albert Einstein published his special theory of relativity in 1905. This theory has been used to explain the odd behavior of electrons and radioactive particles in particle accelerators, the strange behavior of atomic clocks and radioactive particles in motion, and other curious phenomenon involving photons. I will come back to these observations after I discuss the origin of the equation that forms the backbone of special relativity.
The theory of relativity has its roots in an experiment carried out by A. Michelson and E. W. Morley in 1887. They demonstrated experimentally that the velocity of light appears to be the same regardless of the direction it is aimed from a moving source. In this experiment, the velocity of light was measured in reference to Earth’s motion as it orbits the Sun. The instrument used was an interferometer they built on a large slab of sandstone which was floated on a sea of mercury. This made it possible to change the orientation of the instrument and the direction the photons are ejected from their source, and subsequently their direction moving through the interferometer, without disturbing its adjustment. By this means they could compare the velocity of light traveling in various directions. If Earth’s rotation did indeed affect the velocity of the photon, this instrument was easily capable of detecting Earth’s orbital velocity of 29,786 meters per second. The final result of this sensitive experiment indicated that light leaving a source was not influenced by Earth’s rotation as measured in their interferometer.
Of course, this is far different than a bullet short from a moving train. If a bullet is shot in the same direction the train is moving, its velocity is the combined sum of mussel velocity and train velocity; whereas, a bullet shot in the opposite direction is slower because the train’s velocity must be subtracted from mussel velocity. All of this is perfectly reasonable, which caused the scientists at the time to ask why it doesn’t apply to the velocity of light?
The Irish physicist, G. Fitzgerald, suggested that the velocity of light is modified by Earth’s velocity, but cannot be detected in the Michelson-Morley experiment because the length of the instrument (slab of sandstone) shrinks in the direction it is moving. A Dutch physicist by the name of Hendrik Lorentz derived an equation that makes it possible to calculate what the shrinkage would have to be for a given velocity. This article was published in 1892. This equation is known as the Lorentz contraction, and it is always less than one.

Where v is the velocity of the instrument and c is the velocity of light.
Thus, the length of the interferometer would vary according to its velocity with respect to the normal velocity of light as shown in the following equation:

Because the Lorentz contraction is always less than one, the length in motion is always less than the length at rest.
This equation, along with other uses of the Lorentz contraction, forms the basis of the special theory of relativity. I will continue with this discussion in my next blog. Till then be safe and in good health. Kelland—www.vestheory.com
Albert Einstein published his special theory of relativity in 1905. This theory has been used to explain the odd behavior of electrons and radioactive particles in particle accelerators, the strange behavior of atomic clocks and radioactive particles in motion, and other curious phenomenon involving photons. I will come back to these observations after I discuss the origin of the equation that forms the backbone of special relativity.
The theory of relativity has its roots in an experiment carried out by A. Michelson and E. W. Morley in 1887. They demonstrated experimentally that the velocity of light appears to be the same regardless of the direction it is aimed from a moving source. In this experiment, the velocity of light was measured in reference to Earth’s motion as it orbits the Sun. The instrument used was an interferometer they built on a large slab of sandstone which was floated on a sea of mercury. This made it possible to change the orientation of the instrument and the direction the photons are ejected from their source, and subsequently their direction moving through the interferometer, without disturbing its adjustment. By this means they could compare the velocity of light traveling in various directions. If Earth’s rotation did indeed affect the velocity of the photon, this instrument was easily capable of detecting Earth’s orbital velocity of 29,786 meters per second. The final result of this sensitive experiment indicated that light leaving a source was not influenced by Earth’s rotation as measured in their interferometer.
Of course, this is far different than a bullet short from a moving train. If a bullet is shot in the same direction the train is moving, its velocity is the combined sum of mussel velocity and train velocity; whereas, a bullet shot in the opposite direction is slower because the train’s velocity must be subtracted from mussel velocity. All of this is perfectly reasonable, which caused the scientists at the time to ask why it doesn’t apply to the velocity of light?
The Irish physicist, G. Fitzgerald, suggested that the velocity of light is modified by Earth’s velocity, but cannot be detected in the Michelson-Morley experiment because the length of the instrument (slab of sandstone) shrinks in the direction it is moving. A Dutch physicist by the name of Hendrik Lorentz derived an equation that makes it possible to calculate what the shrinkage would have to be for a given velocity. This article was published in 1892. This equation is known as the Lorentz contraction, and it is always less than one.

Where v is the velocity of the instrument and c is the velocity of light.
Thus, the length of the interferometer would vary according to its velocity with respect to the normal velocity of light as shown in the following equation:

Because the Lorentz contraction is always less than one, the length in motion is always less than the length at rest.
This equation, along with other uses of the Lorentz contraction, forms the basis of the special theory of relativity. I will continue with this discussion in my next blog. Till then be safe and in good health. Kelland—www.vestheory.com
Labels:
interferometer,
Michelson-Morley,
speed of light
Monday, February 13, 2012
Normal velocity of photons
The Forces of Nature by Kelland Terry, Ph.D
The balance reached between the photon and a sea of graviton waves traveling in all direction results in a photon with a velocity slightly less than 3 x 10^8 m/s. In contrast an electron in orbit has a velocity of approximately 2 x 10^6 m/s, or even less in the solar wind. There are important differences between photons and electrons that likely explain the difference in their normal velocities even though both are being pushed through space by the same graviton waves.
In contrast to electrons, the two spheres of the photon eject the same string mass per unit time. This means it is always in perfect balance, which allows graviton waves to push it smoothly through space. In addition, the photon has free electons emanating from one sphere, and at the same time, it has an equal mass of free magnons emanating from the other sphere. It seems graviton waves are able to generate more force against free strings than those strings that eventually become bound as complimentary pairs. This would help explain why the normal velocity of photons is higher than the normal velocity of electrons in orbit.
Photons can be as massive as electrons or immensely smaller as in the case of a radio wave photon. Even a photon of visible light can be as much as 10^11 times more massive than a radio wave photon, yet all photons travel at the same velocity even though each makes the same number of strings during the peak of their string cycle. This suggests that an upper limit exists, which holds all photons to the same velocity. This same upper limit also exists for electrons that are forced to travel at high speeds in a particle accelerator. In my next series of blogs, I will begin a discussion of situations where the velocities of electrons and photons are modified by scientists. Till then be safe and in good health. Kelland—www.vestheory.com
The balance reached between the photon and a sea of graviton waves traveling in all direction results in a photon with a velocity slightly less than 3 x 10^8 m/s. In contrast an electron in orbit has a velocity of approximately 2 x 10^6 m/s, or even less in the solar wind. There are important differences between photons and electrons that likely explain the difference in their normal velocities even though both are being pushed through space by the same graviton waves.
In contrast to electrons, the two spheres of the photon eject the same string mass per unit time. This means it is always in perfect balance, which allows graviton waves to push it smoothly through space. In addition, the photon has free electons emanating from one sphere, and at the same time, it has an equal mass of free magnons emanating from the other sphere. It seems graviton waves are able to generate more force against free strings than those strings that eventually become bound as complimentary pairs. This would help explain why the normal velocity of photons is higher than the normal velocity of electrons in orbit.
Photons can be as massive as electrons or immensely smaller as in the case of a radio wave photon. Even a photon of visible light can be as much as 10^11 times more massive than a radio wave photon, yet all photons travel at the same velocity even though each makes the same number of strings during the peak of their string cycle. This suggests that an upper limit exists, which holds all photons to the same velocity. This same upper limit also exists for electrons that are forced to travel at high speeds in a particle accelerator. In my next series of blogs, I will begin a discussion of situations where the velocities of electrons and photons are modified by scientists. Till then be safe and in good health. Kelland—www.vestheory.com
Sunday, February 12, 2012
Normal velocity of the electron
The Forces of Nature by Kelland Terry, Ph.D.
The velocity of the electron in orbit about the proton is 2 x 10^6 m/s. It has the same velocity irrespective of its distance from the proton. This is exactly what we might expect if its velocity is dictated by the balance between opposing graviton waves. In contrast, the velocity of electrons in the solar wind may be as low as 10^5 m/s, yet we must assume both are being driven by graviton waves. I believe the differences can be explained by their orientation in flight.
The electron creates a negative electric field composed of e-electon strings that are not in balance with an equal number of p-electon strings. When the electron is in orbit about the proton, its free e-electons become bound to p-electons emanating from the proton, which allows it to move smoothly through space. Scientists know the electron in orbit only spins either up or down. This suggests that the electron is moving smoothly through space, not tumbling end over end. This is what we might expect if the free e-electons are being created from just one sphere of the electron. This sphere becomes oriented towards the proton when its e-electons become bound to the p-electons emanating from the proton as shown in the following illustration.

Notice, if the electron is coming towards the viewer it only has the option of spinning up or down just as experiments verify.
The electron’s remaining strings are acted upon by graviton waves traveling in both directions, which results in the normal velocity of the electron in orbit. It prevents the electron from spiraling into the proton.
In contrast to this situation, when the electron is moving in the solar wind, its free e-electons cause the electron to be out of balance. One sphere will be acted upon with graviton waves more than the other sphere, which will cause the electron to tumble through space. This will cause the electrons in the solar wind to have less velocity than electrons in orbit about protons.
The velocity of the electron in orbit about the proton is 2 x 10^6 m/s. It has the same velocity irrespective of its distance from the proton. This is exactly what we might expect if its velocity is dictated by the balance between opposing graviton waves. In contrast, the velocity of electrons in the solar wind may be as low as 10^5 m/s, yet we must assume both are being driven by graviton waves. I believe the differences can be explained by their orientation in flight.
The electron creates a negative electric field composed of e-electon strings that are not in balance with an equal number of p-electon strings. When the electron is in orbit about the proton, its free e-electons become bound to p-electons emanating from the proton, which allows it to move smoothly through space. Scientists know the electron in orbit only spins either up or down. This suggests that the electron is moving smoothly through space, not tumbling end over end. This is what we might expect if the free e-electons are being created from just one sphere of the electron. This sphere becomes oriented towards the proton when its e-electons become bound to the p-electons emanating from the proton as shown in the following illustration.

Notice, if the electron is coming towards the viewer it only has the option of spinning up or down just as experiments verify.
The electron’s remaining strings are acted upon by graviton waves traveling in both directions, which results in the normal velocity of the electron in orbit. It prevents the electron from spiraling into the proton.
In contrast to this situation, when the electron is moving in the solar wind, its free e-electons cause the electron to be out of balance. One sphere will be acted upon with graviton waves more than the other sphere, which will cause the electron to tumble through space. This will cause the electrons in the solar wind to have less velocity than electrons in orbit about protons.
Saturday, February 11, 2012
Graviton waves are formidable forces
The Forces of Nature by Kelland Terry, Ph.D.
In a previous discussion, I pointed out that the number of gravitons per unit area may be 10^15 times greater than electons, and 10^25 times greater than magnons. This means there is a sea of graviton waves traveling in all directions that are in intimate contact with the electons and magnons associated with photons and electrons.
In the previous blogs, I assumed the velocity of the graviton waves is 10^23 m/s and magnon and electon waves are 10^15 m/s. Now, if we assume the mass of gravitons in intimate contact with the electons and magnons approaches their mass, then the total momentum of the graviton waves becomes 10^8 times greater than the electon or magnon waves.
These guesstimates suggest that the energy of graviton waves far exceeds that necessary to push either an electron or photon through space.
When the photon is traveling at the speed of light, the large positive force pushing the photon through space is slightly greater than the large negative force. In the case of the electron, the positive forces are slightly greater than the negative forces when the electron is traveling at 2 x 10^6 m/s. At this point, negative and positive forces are at equilibrium. To increase the velocity of the electron higher than 2 x 10^6 requires an outside source of energy.
The great opposing graviton wave forces helps to explain why a small increase in electron velocity meets with great resistance.
In a previous discussion, I pointed out that the number of gravitons per unit area may be 10^15 times greater than electons, and 10^25 times greater than magnons. This means there is a sea of graviton waves traveling in all directions that are in intimate contact with the electons and magnons associated with photons and electrons.
In the previous blogs, I assumed the velocity of the graviton waves is 10^23 m/s and magnon and electon waves are 10^15 m/s. Now, if we assume the mass of gravitons in intimate contact with the electons and magnons approaches their mass, then the total momentum of the graviton waves becomes 10^8 times greater than the electon or magnon waves.
These guesstimates suggest that the energy of graviton waves far exceeds that necessary to push either an electron or photon through space.
When the photon is traveling at the speed of light, the large positive force pushing the photon through space is slightly greater than the large negative force. In the case of the electron, the positive forces are slightly greater than the negative forces when the electron is traveling at 2 x 10^6 m/s. At this point, negative and positive forces are at equilibrium. To increase the velocity of the electron higher than 2 x 10^6 requires an outside source of energy.
The great opposing graviton wave forces helps to explain why a small increase in electron velocity meets with great resistance.
Subscribe to:
Comments (Atom)